«Ты, волна моя, волна!
Ты гульлива и вольна;
Плещешь ты, куда захочешь,
Ты морские камни точишь,
Топишь берег ты земли,
Подымаешь корабли — «
А.С.Пушкин, «Сказка о царе Салтане»
Волновое движение воды имеет нерегулярный характер. Описать это движение аналитически чрезвычайно трудно, а в некоторых фазах – невозможно. Однако существуют теории, основанные на геометрическом и математическом анализе, которые достаточно точно отражают природу реальных волн.
А поскольку океанские волны являются носителями колоссального количества энергии, изучение и количественное измерение волновых характеристик представляет собой, не только крайне сложную, но и весьма актуальную и интересную задачу.
Здесь мы рассмотрим лишь основные понятия, которые, тем не менее, дают достаточно полное представление о многообразных физических процессах, происходящих в волновой среде.
1. Классификация морских волн
Морские волны можно классифицировать по различным признакам.
По силам, вызывающим волновое движение, т. е. по происхождению, в океане (море) можно выделить следующие виды волн: ветровые — вызванные ветром и находящиеся под его воздействием; корабельные — создающиеся при движении корабля и тайфунов; приливные — возникающие под действием периодических сил притяжения Луны и Солнца; анемобарические — связанные с отклонением поверхности океана от положения равновесия под действием ветра и атмосферного давления; сейсмические (цунами) — возникающие в результате динамических процессов, протекающих в земной коре, и в первую очередь подводных землетрясений, а также извержений вулканов, как подводных, так и прибрежных; прибрежные – сейшевые или захваченные волны, рождающиеся у морского побережья с повышенными резонансными свойствами. Практически всегда на поверхности открытых морей и океанов наблюдаются зыбь, ветровые и приливные волны.
По силам, которые стремятся возвратить частицу воды в положение равновесия, различают капиллярные и гравитационные волны. В первом случае восстанавливающей силой является сила поверхностного натяжения, во втором — сила тяжести. Капиллярные волны малы по своим размерам и образуются либо в первый момент воздействия ветра на водную поверхность (рябь), либо на поверхности основных гравитационных волн (вторичные волны). В море главное (силовое) значение имеют гравитационные волны.
По действию силы после образования волны выделяют волны свободные (зыбь), когда сила прекращает действие после образования волны, и вынужденные, когда действие силы не прекращается.
По расположению различают поверхностные волны, возникающие на поверхности моря, и внутренние, возникающие на глубине и почти не проявляющие себя на поверхности.
По форме выделяют двухмерные волны, средняя длина гребня которых во много раз больше средней длины волны, трехмерные, средняя длина гребня которых соизмерима с длиной волны, и уединенные, имеющие только куполообразный гребень и не имеющие подошвы. Если на гребне уединенной волны поместить поплавок, он будет перемещаться вместе с гребнем. Поэтому уединенную волну иногда называют переносной волной.
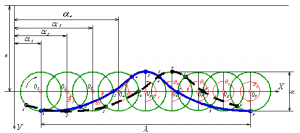
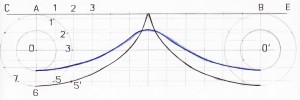
По соотношению длины волны и глубины моря различают короткие волны, у которых длина волны значительно меньше глубины моря, и длинные, у которых, напротив, длина волны значительно больше глубины моря. По перемещению формы волны выделяют волны поступательные, или прогрессивные (Рис. 1), видимая форма которых перемещается в пространстве, и стоячие (Рис.2), узловые линии и вершины которых в пространстве не перемещаются. Прогрессивные волны характеризуются тем, что у них перемещается видимая форма (профиль). Частицы же воды движутся по почти замкнутым орбитам, имеющим форму, близкую к окружности или эллипсу. Любой небольшой предмет, находящийся на поверхности моря, также будет совершать круговые колебательные движения, соответственно движению частиц воды по их орбитам.
Видимое перемещение формы (профиля) волны можно пояснить следующим образом. Предположим, что частицы воды совершают движение по замкнутым круговым орбитам (Рис.1). Если импульс силы, вызывавшей волнение и переместивший частицу воды из точки 1 в точку 1`, действовал слева на право, то частицы, действующие правее частицы 1, придут в движение позже и, поэтому, будут отставать по фазе от частиц, расположенных левее, и займут в момент времени положения 1, 2, 3 … Проведя кривую через эти точки, получим профиль волны в момент времени t1 (сплошная, синяя кривая). Теоретически частицы воды движутся по орбитам с одинаковой угловой скоростью. Поэтому в следующий момент времени t2 они переместятся на своих орбитах на один и тот же угол и займут положения 1′, 2′, 3′ … Проведя пунктирную, чёрную кривую через указанные точки, получим профиль волны в момент времени t2. Как видно на рисунке, профиль волны сместился в направлении действия силы (то есть вдоль координаты х), хотя частицы воды двигались исключительно по круговым орбитам, вокруг собственных неподвижных центров вращения.
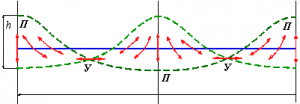
При стоячей волне частицы воды не совершают движений по круговым орбитам (Рис. 2). В пучностях, т. е. в точках, где амплитуда колебания уровня наибольшая, частицы двигаются только по вертикали. В узлах, т. е. в точках, где колебания уровня отсутствуют, частицы двигаются только в горизонтальном направлении. На схеме показаны три положения поверхности моря при стоячих волнах: два крайних (пунктирные линии) и средние (сплошная линия). Буквой У обозначены узловые точки (узлы), а буквой П — пучности. Стрелками на линии среднего уровня показаны орбиты частиц в различных точках волнового профиля.
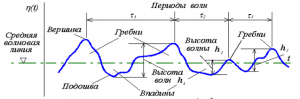
Элементы волны. Каждая волна, поступательная или стоячая, характеризуется определенными элементами. Общими для обоих типов волн являются следующие элементы. Волновой профиль – кривая, получаемая в результате сечения взволнованной поверхности моря вертикальной плоскостью в заданном направлении (обычно в направлении распространения волн). Гребень волны – часть волны, расположенная выше среднего волнового уровня. Вершина волны – наивысшая точка гребня волны. Ложбина волны – часть волны, расположенная ниже среднего волнового уровня. Подошва волны – самая низкая точка ложбины волны.
Высота волны h – превышение высоты волны над соседней подошвой на волновом профиле, проведенном в генеральном направлении распространения волн. Высота волны равна удвоенной амплитуде или удвоенному радиусу орбиты поступательной волны при круговых орбитах. Длина волны – горизонтальное расстояние между вершинами двух смежных гребней на волновом профиле, проведенном в генеральном направлении распространения волн. Крутизна волны – отношение высоты данной волны к ее длине. Крутизна волны в различных точках волнового профиля различна. Для удобства характеристики крутизны волны пользуются отношением высоты к длине
, называемое средней крутизной волны. Частота формы волны:
. Перечисленные элементы определяют геометрические характеристики волны.
Для поступательной волны необходимо добавить еще три элемента. Направление распространения волн, отсчитываемое по часовой стрелке от норда в сторону их движения. Фронт волны – линия на плане взволнованной поверхности, проходящая по вершине гребня данной волны, которая определяется по множеству волновых профилей, проведенных параллельно генеральному направлению распространения волн. Длина гребня волны – протяженность гребня волны в направлении ее фронта. Луч волны – линия, перпендикулярная фронту волны в данной точке.
Кроме элементов, определяющих геометрические характеристики волны, выделяют кинематические элементы. К ним относятся: период волны τ – интервал времени между прохождением двух смежных вершин волн через фиксированную вертикаль. σ = 2π/τ – частота проявления волн во времени (эту же величину ещё обозначают как ώ – угловая скорость трохоидальной волны). Период волны можно определить и как время обращения частицы по ее орбите. Для стоячей волны период определяется промежутком времени, за который совершается полное колебание уровня. Скорость распространения, или фазовая скорость Сф – скорость перемещения гребня волны в направлении ее распространения. За время полного оборота частицы по своей орбите, т. е. за период волны τ , профиль волны сместится на расстояние, равное длине волны λ. Таким образом, определяется фазовая скорость распространения волны Cф = λ/τ. Реальные ветровые волны всегда трехмерные, и для них так же, как и для стоячих волн, затруднительно определить период по скорости перемещения гребня. В этом случае вводится понятие периода волны в одной точке (Рис. 3).
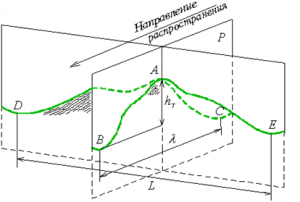
Поэтому для трехмерных волн вводится еще одно дополнительное понятие – высота трехмерных волн. Она находится как разность по вертикали между наивысшим уровнем вершины, определяемым как наивысшая точка гребня волны, расположенного выше среднего волнового уровня, и уровнем подошвы, представляющим самую низкую точку ложбины среднего волнового уровня на переднем по направлению распространения волны её скате (Рис. 4). На схеме трехмерной волны hT – высота трехмерной волны, определяемая как вертикальное расстояние между высотами уровня в точке А (вершина) и В (подошва) профиля волны, λ – длина волны, a L – длина гребня.
2. Теория волн для глубокого моря
Величины соотношений между элементами реальных волн весьма разнообразны. Поэтому при изучении элементов отдельной волны и их изменения обычно используется идеализированная волна, в качестве которой выбирается трохоидальная. Это двухмерная волна, частицы которой вращаются по правильным окружностям. При этом частицы, находящиеся на одной вертикали, колеблются синфазно. Трохоидальная теория волн, иногда называется теорией волн для глубокого моря. Ей более всего соответствуют свободные, гравитационные, поверхностные, двухмерные, короткие, прогрессивные. Именно эти волны мы и рассмотрим вначале, как наиболее интересные с точки зрения их энергетики. В этой теории делаются следующие допущения: • море считается бесконечно глубоким (z → ∞); • жидкость является идеальной, состоящей из отдельных частиц и лишенной сил внутреннего трения; • плотность воды принимается постоянной (ρ = const); • волнение считается двумерным, установившимся и свободным; действие силы, вызвавшей волнение, прекратилось после развития волнения; сами волны рассматриваются как поступательные и гравитационные. Трохоидальный профиль волны заданной высоты и длины можно построить следующим образом. Если окружность радиусом R (рис. 5) катить по горизонтальной прямой (CЕ ), то конец радиуса описывает циклоиду, а остальные точки радиуса описывают трохоиды, соответствующие орбитам с радиусами r = h/2. Волна полной длины образуется после целого оборота катящейся окружности. Принято окружность радиусом R называть катящимся кругом, а радиусом r — производящим кругом.
NB! При построении трохоиды надо иметь ввиду что, катящийся круг катится по прямой, касающейся его верхней точки. Так сказать, «по потолку». При попытке строить циклоиду и трохоиду, перекатывая катящийся круг по прямой, касающейся его нижней точки, вид получающихся кривых не будет соответствовать волновому профилю. И, соответственно, не будут выполняться закономерности, присущие волновому движению. В частности, средний уровень взволнованной поверхности окажется ниже среднего уровня моря. К сожалению, ошибки такого рода нередки даже в научной литературе.
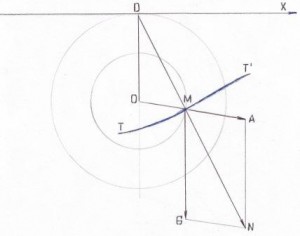
Разделим катящуюся по прямой CЕ окружность на несколько равных частей (на Рис. 5 — на 12 частей). На прямой CЕ отложим длину АВ, равную длине окружности катящегося круга (~R). Тогда при качении круга точки сто окружности 1, 2, 3… будут последовательно совпадать с точками 1, 2, 3… прямой АВ. Чтобы найти точку, где окажется карандаш, установленный в точке б, когда точка 1 окружности совпадет с таковой же на прямой АВ, или, что то же самое, когда центр О передвинется на расстояние А1, проводят через точку 5 катящейся окружности прямую, параллельную АВ, а из точки 1 той же линии опускают перпендикуляр, и от пересечения его с линией, проведенной параллельно АВ, откладывают вправо еще величину половины хорды 5–7 и получают искомую точку 5, принадлежащую циклоиде. (Движение точки 6 при перекатывании катящейся окружности из точки А в точку 1 складывается из поступательного движения на расстояние А1 и вращательного на угол 2π/12). Поступая таким же образом далее, находим, сколько требуется точек циклоиды, соединив которые плавной кривой, получим искомую циклоиду (чёрная линия чертежа). Для построения трохоиды поступают подобным же образом. Трохоида показана на чертеже синим цветом. Нетрудно заметить, что при одной и той же катящейся окружности радиуса R, в зависимости от величины радиуса r производящей окружности, вид трохоиды будет получаться — различный. Здесь можно обратить внимание на одну важную особенность трохоидальной волны. Она не уравновешена относительно прямой линии, соединяющей центры катящейся окружности в положениях А и В (то есть полуволна, находящаяся ниже линии ОО` не равна, по площади сечения, полуволне, находящейся выше этой линии). Более подробно это явление мы рассмотрим при определении потенциальной энергии волны. А пока, рассмотрим трохоиду, образованную катящимся кругом радиусом R и производящим кругом радиусом r (рис. 6).
Пусть в точке М трохоиды t t` находится элементарный объем воды массой m, на который действуют, направленная по отвесу, сила тяжести G G =mg, (1) где g [м/с2] – ускорение свободного падения. В соответствии с принципом Даламбера приложим к элементарному объему воды массой m ещё и центробежную силу А, направленную по радиусу r. A = mω2r , (2) где ω [радиан/с] — угловая скорость элементарного объёма воды в точке М. Из свойств трохоиды следует, что DM является нормалью к ее поверхности. С другой стороны, трохоидальная теория полагает, что каждая трохоидальная поверхность является в то же время и поверхностью равного давления, иначе произошло бы ее смещение в сторону меньшего давления, т. е. возникло бы течение. Из этого предположения следует, что равнодействующая МN сил G и A направлена всегда по нормали к поверхности уровня, то есть к трохоиде. (Поэтому на чертеже, отрезок МN является продолжением отрезка DМ). Важно понимать, вектор МN есть сила, с которой элементарный объем воды массой m давит на поверхность уровня. Соответственно, поверхность уровня давит на элементарный объем воды массой m с силой, характеризующейся вектором NМ, обратным вектору МN, вынуждая его двигаться по окружности. Элементарный объем воды массой m находится в равновесии под действием трёх сил: силы тяжести G, силы инерции А и силы давления поверхности уровня (вектор NМ). Из подобия треугольников MDO и MAN следует соотношение DO/AN = OM/MA (3) Подставляя в (3) выражения (1) и (2) и обозначая соответственно радиусы кругов R и r, получаем R/mg = r/mω2r, что после сокращения даёт соотношение R/g = 1/ω2 , (4) Из этого соотношения легко получить формулы для определения других параметров трохоидальной волны. Поскольку ω = 2π/τ, а длина трохоидальной волны λ равна длине катящегося круга (круга радиуса R) то есть λ=2πR, то, подставляя их значения в выражение (4), получаем формулу для:
длины волны λ = 2πg /ω2 , [м] (5) и
фазовой скорости трохоидальной волны (напомним, фазовая скорость, это скорость перемещения волны в направлении её распространения, то есть вдоль координаты х, на рис. 6)
Cф = λ/τ = , [м/с] (6)
Как видим — фазовая скорость трохоидальной волны определяется ее длиной и не зависит от амплитуды/высоты волны; — со скоростью движения частиц жидкости в волне, фазовая скорость связана неявным образом; — волны большей длины распространяются с большей фазовой скоростью.
Из (5) легко получить соотношения для периода волны τ
τ = , [с] (7)
И для угловой скорости волны ω
ω = , [с -1] (8)
Из приведенных выражений видно, что в них входит только длина волны λ, а высота волны h = 2r вообще не влияет на перечисленные характеристики. С глубиной волнение быстро затухает. Это объясняется тем, что радиусы окружностей, по которым двигаются частицы воды, с увеличением глубины уменьшаются. Тем самым уменьшаются амплитуды колебаний, а, следовательно, и высота волн.
На рис.7 показаны профили волн на поверхности и одновременно на различной глубине.
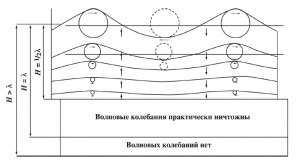
Рис. 7. Изменение профиля трохоидальной волны с глубиной
(Направление движения волны на рисунке: слева направо)
Из рисунка 7 видно, что:
1) гребни и подошвы волны на глубине располагаются под гребнями и подошвами волны на поверхности;
2) длина волн, а значит, их скорость и период с глубиной не меняются;
3) при волнении частицы движутся по круговым орбитам; радиусы орбит, по которым вращаются частицы, уменьшаются с глубиной экспоненциально и тем быстрей, чем короче волна:
r = ro , (9)
где z — вертикальное расстояние вниз от поверхности воды;
Радиус орбиты частиц равен половине высоты волны на данной глубине. Поэтому, заменяя ro =h0/2, получим выражение, определяющее изменение высоты волны с глубиной:
h = h0/2, (10)
где h0 — высота волны на поверхности моря, т.е. соответственно убыванию радиусов орбит частиц убывает и высота волны: Из формулы (10) следует, что на глубине, равной половине длины волны (z = λ/2), высота волны уменьшается в 23 раза, а на глубине, равной длине волны (h =λ) — в 535 раз.
Полученная связь позволяет оценить глубину, на которой волнение практически исчезает. Эта глубина может быть принята равной половине длине волны. Следовательно, можно считать, что на глубине, равной длине волны на поверхности, волнение практически отсутствует. В океане, где ветровые волны, имеют обычно длину не более 100 м, на глубине 50 м волнение практически отсутствует.
4) В соответствии с ( 6 ) скорость распространения волны зависит только от ее длины. С глубиной она не изменяется, так же как не изменяются период и длина волны;
5) Профиль волны представляет трохоиду;
6) Каждая трохоидальная поверхность является в то же время и поверхностью равного давления, иначе произошло бы ее смещение в сторону меньшего давления, т. е. возникло бы течение. Пределы изменения давления при прохождении волны с глубиной уменьшаются пропорционально уменьшению высоты волны. На глубине, равной длине волны, изменения давления исчезающе малы (высота волны уменьшается 535 раз).
3. Энергия и мощность волн
Энергия частиц при волнении складывается из кинетической энергии, не меняющейся при их движении по орбите (производящему кругу трохоиды), и потенциальной, которая меняется, так как при движении по орбите меняется высота частиц над спокойным уровнем.
Если бы центр орбиты частицы совпадал с положением частицы в состоянии покоя, средняя потенциальная энергия за один оборот частицы по орбите была бы равна нулю. Однако в действительности центр орбиты частицы несколько приподнят над положением покоя. Вследствие этого осредненное за период значение потенциальной энергии будет отличаться от нуля, и зависеть от величины превышения центров орбит над положением частиц в покое.
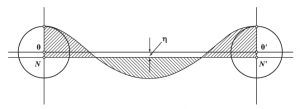
Для определения этого превышения рассмотрим профиль волны, изображенный на рис. 8. Выше уже было упомянуто, что трохоидальная волна не уравновешена относительно прямой линии, соединяющей центры катящейся окружности. Для того, чтобы найти уровень, соответствующий нулевому значению потенциальной энергии, необходимо провести линию NN|, которая делила бы площадь поперечного сечения волны на две равновеликие части. Как показано на рис. 8, эта линия проходит ниже линии OO’, соединяющей центры орбит. Линия NN’ соответствует положению частиц в спокойном состоянии, когда потенциальная энергия равна нулю. Следовательно, ордината ή определяет отклонение среднего положения частиц при волнении относительно состояния покоя.
Таким образом потенциальная энергия элементарного объема воды массой m, будет равна произведению mgή
Математически определено, что среднее превышение частицы ή
для трохоиды ή = πr2/λ. (11)
Отсюда потенциальная энергия ΔEn элементарного объема воды, имеющего массу, равную m, будет равна
ΔEn = [ Дж ] (12).
Найдем теперь кинетическую энергию ΔEk элементарного объема воды массой m . Она равна ΔEk = , где ν — линейная скорость движения частицы по орбите.
ν = r ω , где ω = .
С учётом зависимостей (7) и (8) кинетическая энергия ΔEk элементарного объема воды массой m будет равна ΔEk = =
=
=
или после сокращения:
ΔEk = [ Дж ] (13).
Таким образом, кинетическая энергия элементарного объема воды массой m равна его же потенциальной энергии: ΔEk = ΔEn . Полная энергия равна сумме кинетической и потенциальной энергии, т. е.
ΔE = ΔEk + ΔEn = [ Дж ] (14).
Количество энергии, которым обладает столб воды толщиной db , с основанием, равным единице, и плотностью ρ (получается, что db имеет размерность м3) будет
[ Дж ] (15).
Для получения полной энергии, заключенной в столбе воды с единичным оcнованием, т. е. энергии, приходящейся на единицу поверхности волны, необходимо проинтегрировать это выражение по всей толще от нуля до бесконечности E = (поскольку db имеет размерность м3, интегрирование идёт по объёму), заменяя
, получим:
[Дж/м2] (16).
Теперь, учитывая, что , найдем энергию, приходящуюся на единицу поверхности волны. Принимая, что на поверхности моря высота волны равна
, получим
[Дж/м2] (17).
Из формулы (17) следует, что энергия, заключенная под единичной площадью, зависит только от высоты волны. Квадратическая зависимость указывает на быстрое возрастание энергии при возрастании высоты волны. Поскольку радиусы орбит с глубиной быстро уменьшаются, основная энергия волны сосредоточена на поверхности воды или, другими словами, в верхней части столба воды.
Рассмотрим теперь процесс переноса энергии волнами. Для этого мысленно проведём плоскость, перпендикулярную оси OХ, совпадающей с направлением распространения волны и вычислим поток энергии через полоску этой плоскости, имеющую единичную ширину. Глубину жидкости, для определённости, будем считать бесконечной. Выделим элемент dz этой полосы (ось OZ направлена вертикально вверх) и подсчитаем работу действующих на него сил давления за время dt в направлении ОХ. (Элемент dz в данном случае (dz *1) имеет размерность площади, то есть [м2]. Поэтому, пусть Вас не смущают кажущиеся несоответствия размерностей физических величин, в формулах (17), (18) и (19). Там везде незримо присутствует единица ширины волнового фронта — [м] .)
В гидромеханике установлено, что работа сил давления на всей рассматриваемой бесконечной полоске определяется формулой:
W= ρgπr2 = ρgr2·λ/4 [Дж]
Работа, производимая в единицу времени и равная переносимой энергии волн, или их мощности, будет
N = W/τ = ρgr2 /4 · λ/ τ = ρgr2 /4 · Cф [Дж/с] (18) ,
что с учетом (16) даст:
N = E· Cф/2 [Вт] (19)
Таким образом, в бесконечно-глубокой жидкости полная механическая энергия переносится со скоростью вдвое меньшей фазовой скорости волны.
Подставляя в (19) значение эекргии, заключённой под единичной площадью (17) и фазовой скорости волны в виде (6) и учитывая (7) и то, что r = h/2 получим выражение для мощности, переносимой волной в направлении её распространения, на единицу ширины волнового фронта:
N = ρg2h2τ/32π [Дж/c·м] (20)
Из (20) следует, что мощность, переносимая волнами на глубокой воде, пропорциональна квадрату их амплитуды и периоду.
Поэтому, для волновой энергетики, наибольший интерес представляют длиннопериодные волны большой высоты.
4. Теория волн для мелкого моря. Короткие и длинные волны
В рассмотренной выше, трохоидальной теории влияние глубины моря на волны не учитывалось. Вместе с тем трение о дно существенно изменяет геометрические и кинематические характеристики волн. О величине этих изменений можно судить на основе выводов, даваемых теорией волн для мелкого моря, рассматривающей двухмерное установившееся волнение.
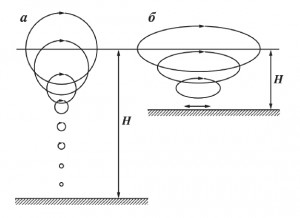
Из формулы (9), r = ro e , следует, что уменьшение радиусов орбит зависит от отношения глубины к длине волны. Поэтому, чем меньше глубина моря и больше длина волны, тем слабее должен меняться радиус орбиты. Но дно препятствует развитию вертикальных колебаний. В результате, при выходе волны на мелководье орбиты частиц принимают эллиптическую форму с большой осью, вытянутой в направлении распространения волны. Размеры осей эллипсов зависят от отношения длины волны к глубине моря и уменьшаются по мере приближения ко дну (Рис. 9 б). А у самого дна вертикальная ось эллипса в то время как горизонтальная его ось сохраняется, то есть частица воды у дна колеблется вдоль горизонтального отрезка прямой.
При очень больших длинах волн (H > 0.5λ) горизонтальная ось эллипса практически не уменьшается с глубиной (Рис. 9 а).
Скорость волны зависит не только от ее длины, но и от глубины моря и выражается формулой
C = , (21)
В случае, когда H/λ велико, гиперболический тангенс стремится к единице th(2πH/λ) ⇒ 1 и формула (21) принимает вид формулы (6),
с = .
Волны, удовлетворяющие отношению H > 0.5 λ, называются короткими. Следовательно, для волн, имеющих длину меньше удвоенной глубины моря, при определении элементов поверхностных волн справедливы формулы трохоидальной теории. К ним относятся ветровые волны, наблюдаемые на некотором удалении от береговой черты.
Для отношений Н/λ < 0.1 значения тангенса и его аргумента с достаточной точностью становятся равными друг другу. Учитывая это, из формулы (21) получают важную формулу для фазовой скорости таких волн:
Сф = , (22)
из которой видно, что скорость распространения этих волн зависит только от глубины моря. Волны, у которых H/ λ < 0.1, называются длинными. Примером длинных волн служат приливные волны.
В интервале отношений Н/λ = 0,5 ÷ 0,1 волны находятся в переходной стадии от коротких к длинным, и их называют волнами мелководья или длинными короткопериодными. К этому виду волн относятся ветровые, распространяющиеся в прибрежной зоне, и цунами.
Вопрос о том, является волна длинной или короткой имеет практическое значение. При подходе волн к прибрежному мелководью они становятся длинными, размывают дно, перемещают огромные массы наносов, изменяя дно и берега. Поэтому для инженерной практики установлены критерии перехода волн от коротких к длинным.
Выводы теории волн для мелкого моря могут быть использованы при изучении приливных волн, для которых хорошо выполняется соотношение (22) и профиль которых близок к синусоидальному. А также частично при изучении ветровых волн и волн зыби при их распространении из открытой части моря к побережью в условиях постепенно уменьшающейся глубины моря.
Важно понять, траектория частиц жидкости в плоских прогрессивных волнах малой амплитуды, как на глубокой воде, так и на мелководье представляют собой замкнутые кривые (окружности или эллипсы). Поэтому перемещения масс жидкости в направлении распространения волн не происходит: распространяется только форма движения. Сами же частицы жидкости совершают малые колебания относительно равновесного положения по замкнутым орбитам.
Следует также иметь в виду важное физическое обстоятельство. Линейная теория, относящаяся к прогрессивным волнам конечной амплитуды, хорошо соответствует только достаточно не крутым волнам. Однако крутизна волны h/λ ограничена предельной формой с острой вершиной (циклоидой), достигнув которой, волна теряет устойчивость и разрушается. Предельная форма волны была исследована Джорджем Габриелем Стоксом, который показал, что максимально возможная относительная высота волны h/λ равна 1/7. Фазовая скорость такой предельной волны на 12% больше скорости волны той же длины, но с малой амплитудой. Это наибольшая теоретически возможная поправка для линейной теории, обусловленная учётом конечности амплитуды волны. Для плоских прогрессивных волн устойчивой формы обычно эта поправка не превышает нескольких процентов. Поэтому для большинства расчетов обычно используют формулы линейной теории волн.
5. Волновые пакеты и групповая скорость волн
Рассмотренные теории морских волн относятся к простым системам волн, имеющим на всем пространстве одинаковые высоты и периоды (длины). В природе никогда не наблюдается такая система. Волны всегда представляют собой сумму того или иного количества простых волн, распространяющихся в различных направлениях и имеющие различные высоты и периоды.
Простейшим случаем системы волн является наложение (интерференция) волн, близких между собой по периоду и высоте, распространяющихся в одном направлении. Результат интерференции двух таких волн представлен на рис. 10. Пунктиром показаны интерферирующие волны, черной сплошной линией — результирующая волна, а тонкой сплошной линией — ее огибающая. Как видно на рисунке, огибающая охватывает несколько результирующих волн, изменяющих свою высоту от почти нулевых значений до наибольшей в данной совокупности, называемой группой волн.
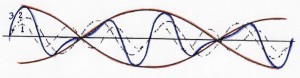
Рис. 10. Схема наложения (интерференции) волн. 1 и 2 — интерферирующие волны; 3 (синяя) — результирующая волна; оранжевая — волновой пакет
Интерференция волн приводит к появлению явления, известного под именем «девятый вал», когда через несколько постепенно нарастаюших по высоте волн приходит особенно высокая волна, которую и называют девятым валом. После этого высота волн начинает уменьшаться почти до состояния спокойного моря, а затем снова начинает возрастать.
Самая крупная в групповом пакете волна в динамике своего движения всегда проявляется как малоподвижная или стоячая волна. Девятый вал может иметь удвоенную высоту в сравнении с прогрессивной волной, отчего его угол склона вблизи гребня может достигать 60°.
Следует также понимать, что хотя явление групповых волн и носит название «девятый вал», однако наибольшая по высоте волна может быть , в зависимости от периодов интерферирующих волн, любой, а не только девятой.
Огибающая группы волн, называемая волновым пакетом, перемещается вместе с перемещением результирующей волны. Однако скорость ее перемещения, которая определяет скорость перемещения группы волн Сгр и называемая групповой скоростью, не совпадает с фазовой скоростью интерферирующих волн С1 и С2.
В случае глубокого моря между этими скоростями существует следующая связь:
Cгр = С1С2/С1+С2 (23)
Так как периоды интерферирующие ветровых волн в глубоком море часто близки между собой, можно принять C1 и C2 равными их средней скорости C, что дает
Cгр = С/2 (24)
Следовательно, для волн глубокого моря можно принять групповую скорость волн или скорость перемещения волнового пакета, равной половине фазовой скорости составляющих его волн.
Для волн мелководного моря групповая скорость зависит от отношения глубины моря H к длине волны λ .
Групповая скорость волн непосредственно определяет скорость переноса энергии в направлении их распространения и входит в уравнение баланса энергии волн.
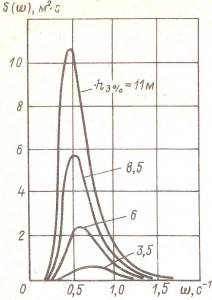
В таблице 1 приведены экстремальные оценки для морских волн с периодами от 1 до 15 секунд. Amax соответствует прогрессивной волне с обрушающимся гребнем, в котором поток воды движется со скоростью, равной фазовой скорости фронта волны С. Важно отметить, что свежие ветровые волны, с ярко выраженной групповой структурой, могут быть существенно выше, чем показанные в таблице 1.
Для морских акваторий характерными являются периоды волн от 6 до 8 секунд (выделено синим), что соответствует длине волны порядка 80 м, максимальной скорости потока в гребне волны — 10 м/с (20 узлов) и экстремальной амплитуде волны порядка 10 м. В открытом океане период волн может достигать 15 и более секунд, но только для волн зыби, имеющих относительно малую амплитуду, обычно без обрушающихся гребней.
На побережье открытого океана, при прохождении штормов, нередко наблюдаются волны прибойной зыби с периодами порядка 11-13 секунд (выделено красным), высота которых существенно выше, чем у волн открытого моря. Именно поэтому плавание вблизи побережья или над морскими отмелями всегда представляет повышенную опасность для мореплавателей.
6. Волновое течение
В глубоком море (при H > 0.5 λ), согласно трохоидальной теории, возникают волны, профиль которых описывается трохоидой, а частицы движутся по замкнутым круговым орбитам.
В действительности же, как показывают наблюдения, частицы имеют и поступательное движение, которое называется волновым течением. Оно возникает независимо от того, есть ли ветер или нет его, т. е. обусловлено природой самого явления.
Теория возникновения волнового течения была разработана академиком В. В. Шулейкиным в 1954 году.
Скорость поступательного движения частиц, т. е. скорость волнового течения, за период волны изменяется. Она также неравномерна как вдоль длины волны, так и по глубине. Скорость максимальна на середине склона волны и уменьшается с глубиной. Осредненная за период волны скорость волнового течения Vв на поверхности выражается формулой Стокса через радиус орбиты частицы на поверхности ro, её скорость с и длину волны λ
Vв = r02·(2π/λ)2c , (25)
Так как радиус орбит частиц убывает с глубиной по экспоненциальному закону r = ro , то скорость волнового течения Vвz на глубине z определяется формулой
Vвz = r02(2π/λ)2c , (26)
Таким образом, средняя ее величина за полный период волны зависит от высоты и длины волны и быстро уменьшается с глубиной , но на поверхности океана может быть существенной.
Волновое течение также изменяет орбитальное движение частиц и вызывает отклонение профиля волны от трохоиды. Профиль волны при наличии волнового течения отличается от трохоиды большим заострением гребня и притупленной впадиной.
7. Общее представление о спектральном методе в теории волн
Рассмотрим теперь, что получится, если принцип наложения применить к прогрессивным волнам с различными амплитудами и существенно отличающимися частотами, распространяющимся в одном направлении. Профиль результирующей волны будет иметь вид, характерный для нерегулярного, ветрового волнения. Подвергнув запись волнового профиля гармониче6скому анализу можно убедиться, что результирующая кривая представима в виде суммы некоторого числа простых гармонических составляющих – прогрессивных волн с кратными частотами и различными амплитудами. Такая суперпозиция лежит в основе спектрального метода изучения и расчёта морского ветрового волнения.
Сложив всего три плоские прогрессивные волны с различными амплитудами и кратными частотами, но с одинаковым направлением распространения dх и с нулевой начальной фазой, получим результирующий профиль, который хорошо имитирует запись ветрового волнения в точке (см. Рис. 3.). По крайней мере, с качественной стороны. Увеличивая число гармонических составляющих и, придавая им разные начальные фазы, можно получить всё более точное представление истинного профиля реального морского волнения, если оно имеет двухмерный характер, то есть длины гребней волн очень велики.
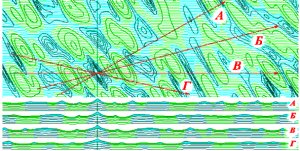
Ещё сложнее оказывается картина при наложении волн, распространяющихся в разных направлениях. Для моделирования реальной картины штормового волнения в открытом море можно попытаться наложить друг на друга ячеисто-групповые структуры ветровых волн и волн зыби, характеристики которых могут отличаться либо длинами волн, либо направлением их распространения. Полученная волновая картина (рис. 11) вполне соответствует наблюдениям за реальным штормовым волнением в открытом море.
Модель трехмерного волнового поля для открытого моря (Рис. 11.), представляет собой наложение трех независимо существующих ячеисто-групповых систем волн: 1) ветрового волнения: λ=60м, τ=6,2с, h=7,2м, движущимся в направлении A=250°; 2) первой системой волн зыби: λ=100м, τ=8,0с, h=5,9м, A=210°; и 3) второй системой волн зыби: λ=160м, τ=10,1с, h=5,1м, A=270°. Показаны профили волн и изолинии уровней моря. Зеленым цветом прорисованы впадины волн, голубым – гребни. Изолинии уровня моря проведены через 2 метра. Курс движения судна в направлении А ведет навстречу ветровому волнению, курсы Б, В и Г – на 15°, 30° и 45° вразрез волне. В нижней части рисунка показаны профили волн на отмеченных курсах.
На Рис. 12 показана волновая поверхность, получающаяся как результат наложения большого числа ветровых волн с различными длинами и направлениями распространения.
Для полной количественной оценки столь сложной картины волнения, необходимо знать амплитуду и начальную фазу каждой гармонической составляющей, распространяющейся в определённом направлении. При бесконечно большом числе составляющих непосредственное определение этих элементов, очевидно, крайне затруднительно. Поэтому количественные оценки волнения производятся в рамках спектрального метода особым путём – с помощью энергетических соотношений.
Поскольку полная механическая энергия плоской прогрессивной волны, приходящаяся на единицу длины её гребня, пропорциональна квадрату её амплитуды, энергию каждой i-той гармонической составляющей волнения, имеющей j-тое направление распространения можно представить, согласно (16), в виде
Еij = ρgrij2/2 , откуда амплитуда гармоники
Aij = , (27)
Но энергию, приходящуюся на каждую гармоническую составляющую спектра, можно подсчитать и другим способом.
Представим себе элементарный участок поверхности моря, на границах которого расположены системы прогрессивных волн с частотами от ώ до ώ + Δώ и с направлениями распространения от u до u + Δu. Обозначим через s удельную энергию волн – количество энергии, приходящейся на единицу площади поверхности моря. Величина s зависит от того, какая из гармонических составляющих волнения располагается на выделенной единичной площадке, т.е. s = s (ώ, u). Тогда энергия i-той гармонической составляющей с j-тым направлением, приходящаяся на бесконечно малый интервал частот Δώ и направлений распространения Δu, будет равна Еij = S (ω, u)ΔώΔu . С учётом (27) амплитуда этой составляющей
Aij =
Обозначив S = s (ω, u) / ρg можно записать
Aij = , (28),
то есть определять амплитуды гармонических составляющих через его удельную энергию. Функция S(ώ, u), характеризующая распределение удельной энергии волн по частотам и направления распространения, называется двухмерной спектральной плотностью волнения или двухмерным энергетическим спектром. Если эту функцию проинтегрировать по всем возможным углам u, например от 0 до 2π, то получим одномерный энергетический спектр, называемый также частотным. В гидромеханике, с помощью двухмерного энергетического спектра принято количественно оценивать трёхмерное морское волнение, а с помощью частотного – двухмерное. Спектральная плотность измеряется в квадратных метрах в секунду.
Примерный вид зависимости частотного спектра от спектральной частоты представлен на рис. 13.
Из теоретического описания закономерностей зарождения, развития и разрушения морских волн становится ясно сколь сложно создать устройство, которое было бы в состоянии использовать энергию переносимую волнами для совершения полезной работы. И при этом не было бы разрушено этой энергией.
Видео, которое, я надеюсь, поможет Вам продолжить свой путь, в познании этого удивительного явления природы, было сделано Jean-Rene Keruzore (Air Vide Et Eau). На экране запечатлен ураган Йоахим, обрушившийся на побережье Бретани, 16-го декабря 2011 года. Штормовые волны вылизывают маяки на скалах морской гряды Армориканского горного массива. Сила воды была в тот день такая, что мальтийский сухогруз «ТК Бремен» оказался не в состоянии ей сопротивляться, и выброшен на мель пляжа.
На первый взгляд жуть! Но подумайте о том, что возобновляемая энергия волн, насыщая воду океана кислородом, несёт энергию жизни её обитателям. Шторм — это живая энергия океана. Незавидная участь сухогруза «ТК Бремен» ждёт и Человечество, если оно будет и дальше корчить из себя повелителя Природы, вместо того, чтобы учиться жить в согласии с Ней.
А каково Ваше мнение?
Пишите в комментариях!